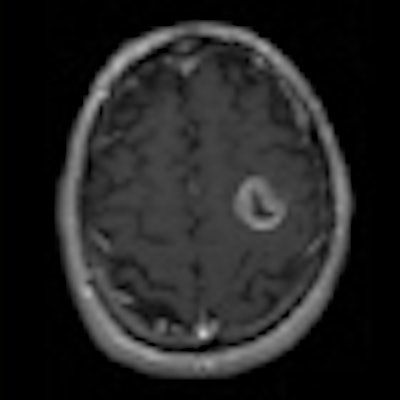
In an attempt to personalize treatment regimes, a research team from the University of Washington in Seattle has developed a mathematical model for predicting untreated glioma growth. The model is based on the hypothesis that growth can be quantified by two net rates: proliferation and invasion, with MRI data used to estimate these parameters for an individual patient. Now, the researchers have extended the model to incorporate the effects of external-beam radiation therapy (Physics in Medicine and Biology, June 21, 2010, Vol. 55:12, pp. 3271-3286).
"We are applying mathematical modeling techniques built upon routine clinical data already available to clinicians -- such as MRI and PET -- to help improve outcome for patients," explained lead author Kristin Swanson. "Such personalized medicine approaches are essential to ensure that patients receive therapies that are most appropriate to their specific tumor and not that of the average tumor in a group of patients."
Response prediction
To incorporate the effects of radiotherapy into their existing glioma growth model, the researchers employed the widely used linear quadratic model for radiation efficacy. This model can be used to calculate effective dose and cell survival probability based upon an individual treatment plan and a radiobiologic response parameter (α) that quantifies the patient's degree of response to radiotherapy.
 |
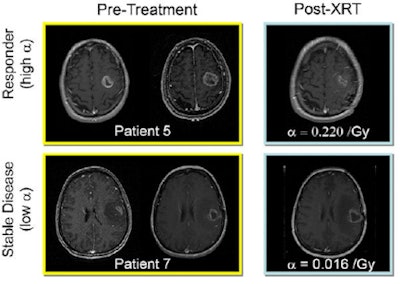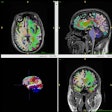
| Response to therapy is conventionally assessed by determining changes in gross tumor volume on MRI prior to and after the administration of therapy. Postcontrast T1-weighted MRI images are shown for two glioblastoma patients who would typically be separated into generic groups: responder and stable disease. The radiation response parameter α gives an additional quantification of radiation response for each patient. Image courtesy of Physics in Medicine and Biology. |
The enhanced model was tested on nine histologically diagnosed glioblastoma patients. All patients underwent at least two pretreatment and one post-therapy MRI exam (postcontrast T1-weighted [T1Gd] and T2-weighted). Tumor growth velocity was estimated from the change in tumor radius between two pretreatment MR images (spaced by a minimum of five days). This growth velocity, together with a tumor cell gradient inferred by comparing the T1Gd and T2 images, was used to calculate proliferation and invasion values for each patient -- thus uniquely characterizing that glioma's untreated growth kinetics.
The MRI-derived parameters were used to create a virtual tumor for each patient, which was then "treated" with the same radiation dose and fractionated radiotherapy plan as clinically prescribed. To estimate the parameter α for each patient, the researchers simulated radiotherapy using a range of α values. The difference between simulated and observed tumor radii (at the first post-treatment MRI) was recorded and data regression performed to yield a value of α that minimized this difference.
The researchers saw that each patient's radiation response parameter was strongly correlated to their tumor's pretreatment net proliferation rate -- which is not unexpected as actively proliferating cells are more susceptible to irradiation -- and that the computed α values lay within published ranges. They note that α was not correlated to the rate of invasion, suggesting that tumor response may be independent of the degree of invasiveness.
This ability to predict α from the proliferation rate was confirmed using a leave-one-out cross-validation technique, which gave median errors (difference in post-therapy tumor radius between simulation and MRI data) of 2.4 and 4.5 mm for T1Gd and T2 MR images, respectively.
As tumor proliferation rate can be assessed prior to treatment, these results imply that pretreatment MRI can also be used to estimate α. Thus it should be possible to determine in advance whether a patient is likely to respond to therapy. "The metric for this investigation was the ability to predict the post-treatment tumor size," explained co-researcher Russell Rockne. "But the real success was that the prediction could be achieved using only routine clinical information prior to treatment."
Looking ahead
The researchers are currently using the model to analyze pre- and post-treatment growth dynamics in further gliomas, as part of a prospective research study including more than 300 patients. And although the mathematical model could actually be applied to any highly invasive tumor, Rockne points out that it could make a real clinical impact in the case of glioma, due to the limitations of current imaging-based response monitoring. "Any increase in survival or improvement in the management of this disease is a significant advance," he said.
The model is now being developed to include focal radiotherapy resistance, by adding an oxygen enhancement ratio based on regions of hypoxia as defined by PET imaging. "Preliminary data indicate that the accuracy of the model's prediction of glioma response to radiotherapy is improved by incorporating focal areas of treatment resistance," said Swanson. "We hope to collaborate with a variety of national clinical trials that focus on incorporating PET imaging in radiation treatment planning."
By Tami Freeman
Medicalphysicsweb editor
July 12, 2010
Related Reading
Hypofractionated stereotactic RT ups survival for glioma patients, June 16, 2010
Neuroimaging and genomics characterize glioblastoma noninvasively, March 31, 2008
© IOP Publishing Limited. Republished with permission from medicalphysicsweb, a community Web site covering fundamental research and emerging technologies in medical imaging and radiation therapy.
